众所周知，现实中任何事都没有绝对的，只有发生的概率。

本文主要从概率的角度得出该如何决策。下面列出几个场景：

1. 决策的基石：凯利(Kelly)公式

一次次的猜硬币怎样赢的最快

场景：质量不均匀的硬币，正面概率为p反面概率为q,赢后多给x倍本金,输后扣除后为y倍本金,初始本金为G0,参与次数N,下注比例f. 其中 p+q=1,x>=0,1>=y>0

赌很N次后剩余的本金: $$ G=G0\times (1+f\times x)^{p\times N}\times (1-f\times y)^{q\times N} $$

最优下注比例f：就是 G(f)的最大值，此式导数=0,且二阶导数小于0.

原式取对数: $$ln(G)=ln(G0)+(N\times p)\times ln(1+f\times x)+(N\times q)\times ln(1-f\times y)$$

$$ln(G/G0)/N=p\times ln(1+f\times x)+q\times ln(1-f\times y) （式1）$$ （式1）的二阶导数：

$$ -\frac{x^2\times p}{(1+f\times x)^2}-\frac{y^2\times (1-p)}{(1-f\times y)^2} $$

分式都为正，所以小于0，满足最优下注比例的条件。

由（式1）的一阶导数=0

$$\frac{x\times p}{1+f\times x}-\frac{y\times (1-p)}{1-f\times y}=0$$

得：f=p/y-(1-p)/x （式2）

单次收益的期望值是：E(r)=px-(1-p)y（式3）

输赢差异：$$\Delta=x+y$$

收益的方差$$var(r)=p\times q\times \Delta^2 （式4）$$

和最优下注份额的关系：f=E(r)/x/y（式5）

长期最优下注比的单次增益：g=E(r)/x/ypx-E(r)/x/yqy=E(r)*(p/y-q/x)（式6）

式5的意义是期望和下注比例同号：期望为正做多，期望为负做空，这样肯定能赢。

但即使期望值为正，如果f并非式5的值，式1仍有可能小于0，即赔钱。

现实必有一次赔光的可能性即y=1,q>0时。

此时下述比例为：f=1-q-(q)/x=1-q*(1+1/x)<1，即永远不能满仓。

2. 简单的效果提升：赌注分M份同时猜M场硬币能赢多少

这个场景相当于二项式分布，当二项式的M足够大时可以用高斯分布来近似。

M份同时猜M场时收益的期望为：E(rm)=E(r)

M份同时猜M场时收益的方差为：

$$var(rm)=\frac{1}{M^2}\times \sum_{i=1}^{M}var(r_i)=\frac{1}{M}\times var(r)$$

收益分布函数为正太函数： N(E(rm),var(rm)) （式7） 对收益大于零的场次和收益小于0 的场次做统计， M次博弈统计新 x_m,y_m，p_m,q_m成了单次x,y,p,q的函数。

$$p_m=\int_{0}^{\infty} N(E(rm),var(rm)) dz$$

$$q_m=\int_{-\infty}^{0} N(E(rm),var(rm)) dz$$

$$x_m=\int_{0}^{\infty} N(E(rm),var(rm))\times z dz$$

$$y_m=\int_{-\infty}^{0} N(E(rm),var(rm))\times z dz$$

$$fm=E(rm)/x_m/y_m$$

M趋向无穷大时有，方差var(rm)为0，收益是一个无风险的稳定的期望值（式3）

同样猜一枚相同的硬币，同时猜了多次就可以提高期望值（式6）到（式3）

空间上分成M份博弈有一个上限E(rm)=E(r), 但时间上博弈N次，却可以远远高于E(r)

3. 利润无上限的特殊场景：可以同时赌正反面的赌局

Dutch Book，有叫荷兰赌的，有叫大弃赌的。

这种场景的本质是同时参与多个相关性的结果，且至少有一种结果压对压错是不公平的。

设:压正面猜对得,猜错损失；压反面猜对得,猜错损失 分别为 $$x_z,y_z,y_f,x_f$$ 这里当$$x_z=x_f,y_z=y_f$$时，就是公平的结果，就不可能套利了。

在这个场景，结果为正面就不可能是反面，所以是相关的。策略是同时即赌正面也赌反面。

假设拿出一部分资金，正面下注，反面下注的份额 为 $$f_z，f_f, f_f+f_z=1$$

类比式一得到对数收益：$$p\times ln(1+f_z\times x_z-f_f\times y_z)+q\times ln(1+f_f\times y_f-f_z\times x_f)$$ 取导数为0时的正反面最优下注份额（不是总资金的份额，而是下注正反面分别占的比重） $$ f_z=\frac{p\times (1+y_f)}{x_f+y_f}-\frac{q\times (1-y_z)}{x_z+y_z} \\ f_f=1-f_z $$ 此时结果为正面时单次收益为： $$e_z=f_z\times x_z-f_f\times y_z$$ 此时结果为反面时单次收益为： $$e_f=f_f\times y_f-f_z\times x_f$$

当有最优下注时，$$e_z=e_f$$

既然压正收益=压负收益大于0，就相当于于无风险。 把这种压法的结果看成一个新的赌局。 即 $$p_n=1,x=e_z=e_f;q_n=0,y=0;$$

根据式5，得出最优的下注比例 $$f_n=e_z/e_z/0=无穷大倍的本金（式8）$$

综上为了尽可能高的加快收益，杠杆无限大，分配的比例为压正面的比率为f_z,剩下的全压反面。

4.精细的效果提升：多次玩N个质量不均匀的有M个面的骰子

多次玩N个不同，且质量不均匀的有M个面的骰子。一个骰子代表一个标的有多种不同的收益。N个骰子代表有N个标的事件。

当你知道这些筛子的历史表现数据（客观相关性），相当于了解了偏向性不同的资产标的。

按历史表现（经验），用不同份额w买N个骰子。期望收益值如下

$$ E=\sum_{i=1}^{N}w_i\times E （式9）\\ \sum_{i=1}^{N}w_i=1 $$ $$\sigma_p^2=\sum_{i=1}^{N}\sum_{j=1}^{N}Cov_{ij}w_i\times w_j=\sum_{i=1}^{N}w_i^2\times \sigma_i^2+2\times \sum_{*}Cov_{ij}w{i}\times w{j} （式10）$$ 当只有2个标的时 $$Var=w_1^2\times \sigma_1^2+w_2^2\times \sigma_2^2+2\rho w_1w_2\sigma_1\sigma_2$$ $$\rho 是相关系数。$$

这是一个平方展开式， $$当-1<=\rho<=1时取值不同时，(w_1\sigma_1-w_2\sigma_2)^2<=Var<=(w_1\sigma_1+w_2\sigma_2)^2$$ 波动最小时有可能为0

同理N个标的也可以得出，该组合下E和Var的数值。我们这里用正太分布来近似二项式分布，算一下指定期望值和方差下的增长的速度。 $$G = \int N(E,\sigma^2)\times ln(1+z)dz$$ z=-1的损失增大，具体博弈时不会参与损失超过本金的场景，意味着只有部分区间的正太函数对积分有贡献。 因为在正太分布方差较大时，发生在z=-1处的概率会增加，这时G变为负无穷，意味着破产。

这个积分表达式我不知道有没有简单的解析形式，也许做量化的人会有答案，欢迎评论区指点一下。

我这里就直接写个程序求数值解了，横轴为期望，纵轴为方差。期望小方差大的向左上扭曲的曲线属于超出公式近似试用范围的，应该用真实的分布函数（二项式）来代替。 我这里是通用的数值求解场景，积分范围仅限于4标准差之内，在z=-1处有一个截断（二项式分布无需作此限制）。只考虑向右上测扭曲的等高线部分就可以了。

绘制图如下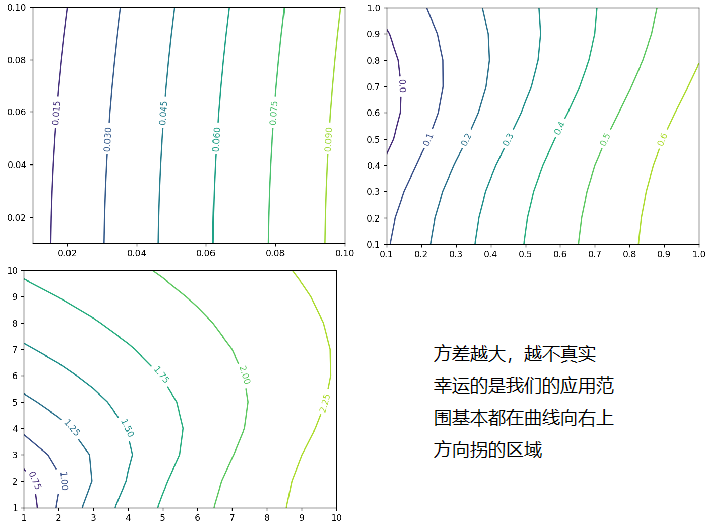： 结论：自变量分别是期望和方差，相同期望之下方差越小G越大。

三维图中，G的值用高度图表示，是一个类似等高线的图。最高点位于E无穷大，方差为0时。取值范围为第一象限。

具体组合场景下 期望和方差（式9,式10）为取自变量值的范围，该范围在图上值的最大点，对应此时各标的组合的最优权重。

这种组合的一个特殊场景就是文本的第二部分，即方差相关性为0（随机）的场景。

只要信息不对称的情况，博弈个体就可以利用这个信息在这个图上找出更真实的期望和方差（式9,式10）的位置，也就是意识到有低风险高收益的情况或该清仓了。

内幕，个体灵活性不同，体量大小，设备速度，这些差异，相当于不同博弈个体在3维图上的自变量范围不同。

5.具体场景下对上式的应用：

5.1 p,q是客观概率，而人对标的的判断为主观概率，永远都有全部损失的时候，所以永远不能满仓。

现实中荷兰赌通常有2种情况

• 一种就是直接利用不同下注人对同一事物的对立面的不同判断来获取利差。
• 另一种比较隐晦，做对冲的通常选择趋势一致的不同标的作为对立面。这种场景不太严格，大家相信这个规律，但现实有时会背离规律，这样加杠杆的先决条件就失效了，或者要被平仓，也可能是一个获利的机会。

5.2加杠杆这个机构普遍采用的做法，貌似跟永远不能满仓矛盾。

这些机构的加杠杆和（式8）的杠杆有些不同。

对冲的杠杆只是针对他们资金的一部分来操作的，这一部分保证金的杠杆倍，相当于标的标值的上限。

因为到反方向超过杠杆的倍数会自动清空，不影响保证金之外的资金(暂时不考虑清仓不及时导致的后期补偿)，所以机构的资金使用方式相当于不满仓，部分资金靠杠杆自动止损。

5.3现实中还有一个现象，跟永远不能满仓的结论矛盾。

比如有的人做生意会借钱，许多人都成功了（银行的贷款抵押相当于自己的东西，暂时不考虑这个场景）。为了安全永远也不能借超过自己资产的钱吗？

广义上的资本不限于真金白银，如何使用就因人而异了，这个没有标准答案。

跟机会成本相关的一个场景：自己现在只有100元，打工每年挣10元，一个看好的创业项目需要投入200元，可以每年挣100元。

假如借100元创业后，3年后就奔小康了。假如打工需要10年后才能到凑够创业资本，就损失了8年的高利润收益。

借款相当于透支余生的收入，选择了未来的时间点作为总收益的观察基准。

如果创业者评估1/4的概率创业成功，成功后认为这个企业可以持续10年。

那么未来10年的期望收益就是0.25 x 1000-0.75 x 200=100

这跟他打工10年获得稳定100元的期望相同。

换句话说，如果他理性，觉得成功概率小于25%就不应该辞职打工

这里只考虑了失败，但没考虑损失和收益形成的方差，较为准确的评估应该使用G(E,var)的三维图。

不过既然收益也是猜的，持续时间也是猜的，那么太精确的分析也没有意义，通常每个人只靠感觉就下了判断。

欢迎评论区留言交流。